Множества могут быть пустыми, например, люди старше 200 лет. Такое множество обозначается знаком Ø. Кроме того, множества могут быть бесконечными, например, множество целых чисел.

Более формально: множество задается некоторым логическим высказыванием, которое истинно для всех его элементов. Поскольку логическое высказывание можно формализовать, то можно сказать, что множество задается некоторой логической функцией.

Как изображают множества?

Множества принято изображать с помощью кругов Эйлера – диаграмм, которые используются для визуального представления отношений между множествами. Их придумал Леонард Эйлер в середине XVIII века. Каждое множество обозначается своей областью – кругом или другой фигурой.

На примере ниже показаны следующие множества:

А - натуральные числа меньше 5: {1, 2, 3, 4}.

B - натуральные числа больше 5 и меньше 10: {6, 7, 8, 9}.

Таким образом, число 5 не входит ни в одно из множеств, поэтому находится вне круга.

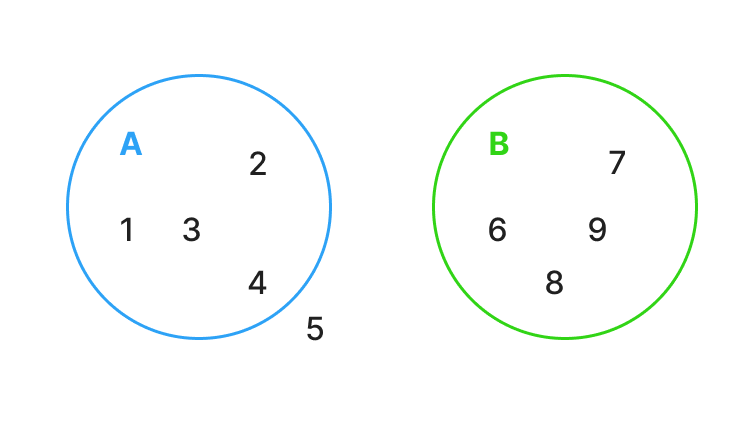
Пример отображения множеств в виде диаграмм Эйлера

Какие операции можно совершать с множествами?

Пусть есть какие-то два множества X и Y, тогда:

Множество, элементы которого не входят в X, но входят в Y, называется дополнением X до Y.

Множество, элементы которого входят и в Y, и в X, называется пересечением X и Y.

Множество, элементы которого входят или в Y, или в X, называется объединением X и Y.

Рассмотрим эти операции на примере следующих множеств:

Дополнением множества A до множества D является множество E = {5, 6, 7}, поскольку элементы 5, 6, 7 не входят в А, но входят в D.

Пересечением множеств A и B является множество F = {2, 4}, поскольку только элементы 2 и 4 входят в А и входят в B.

Объединением множеств С и B является множество G = {2, 3, 4, 5, 6, 7}, поскольку элементы 2, 4, 6 входят в B, а элементы 3, 5, 7 входят в C.

Как показывать операции на диаграммах Эйлера?

Для примера воспользуемся уже определёнными выше множествами:

На диаграмме Эйлера они выглядят так:

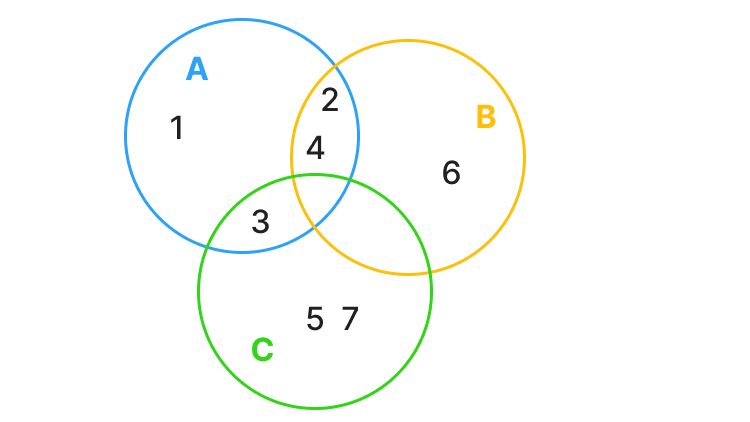
Пример отображения операции на диаграммах Эйлера

На рисунке ниже синим цветом обозначено пересечение множества А и B. Это область, которая находится и внутри круга множества А, и внутри круга множества В:

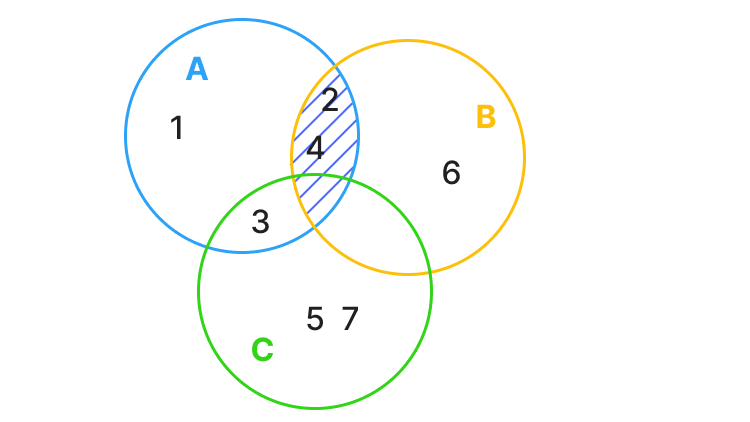
Пересечение множеств А и B

На рисунке ниже синим цветом обозначено объединение множества С и B. Это область, которая находится внутри круга множества С, а также внутри круга множества В:

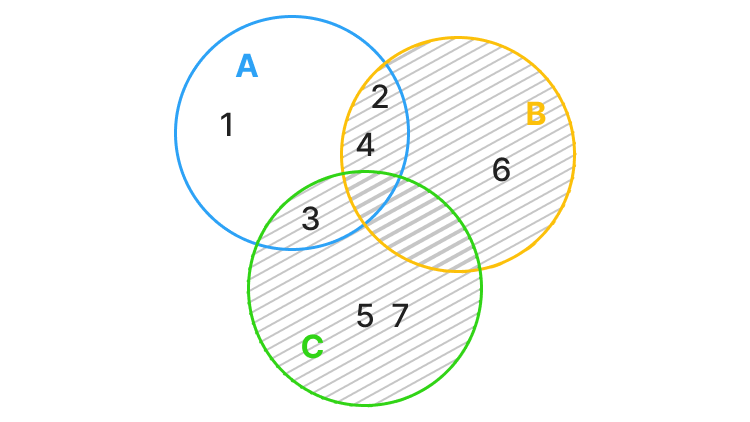
Объединение множеств С и B

Заключение

Множество – это фундаментальная концепция, позволяющая организовать и классифицировать объекты. Оно представляет собой набор неповторяющихся элементов, который может быть конечным, бесконечным или пустым. Множества можно определить заданием условия, которое истинно для всех элементов, входящих в это множество и ложно для элементов, не входящих в него.

Дополнение, пересечение и объединение – это операции над множествами, которые позволяют создавать новые множества из существующих. Дополнение множества – это все элементы, не входящие в него. Пересечение – это элементы являющиеся общими для двух множеств. Объединение – это все элементы, которые принадлежат хотя бы одному из двух множеств.

Для представления множеств и операций над ними в виде рисунка используются диаграммы Эйлера. В них каждое множество изображается кругом. Эти диаграммы позволяют визуализировать операции над множествами.

Остались вопросы?

Расскажите нам, что вызвало трудности, и мы ответим на ваш вопрос по элеткронной почте